2024-07-18 服务与支持 浏览 159
传统的电磁流量计是依据法拉第电磁感应定律制成的导电介质体积流量测量仪表，在石油、化工、冶金和造纸等行业应用极为广泛，但是仅仅适用于对流速稳定的导电流体进行测量，极大地限制了电磁流量计在流量测量领域的使用。针对这一缺陷，诸多学者对其进行了研究，并取得了一定的研究成果，如较之于传统的采用扇叶切割磁感线的方法，提出的采用高磁导率的小球切割磁感线的技术，解决了无法测量低导电率的液体的难题，并实现了双向测量。在实际应用中，由于电磁流量计工作原理的限制，流量计输出信号微弱，淹没在各种噪声中。因此，如何将流量信号与各种干扰信号有效分离是进一步提高电磁流量计测量精度的关键。传统方法采用模拟低通滤波器滤除输出信号中的高频噪声，但是模拟滤波器动态响应无法调整，同时硬件电路本身也会引入噪声。小波分析具有多分辨率分析的特点，具有良好的时－频特性，从而为其在信号降噪中的应用提供了广阔的前景。针对模拟滤波器去噪的缺点，本文将小波阈值去噪方法引入新型电磁流量计输出信号处理中，降低了流量计信号中的噪声，提高了测量精度。
1 新型双向电磁流量计介绍
1.1 新型双向电磁流量计模型
新型双向流量计如图1所示，较之于传统的电磁流量计，它可以测量低导电率的液体，实现双向测量，极大地提高了测量精度和测量工序。
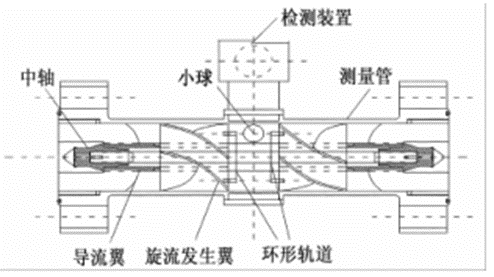
图1 新型双向流量计结构图
当被测流体经过分流叶片进入旋流器后，带动高导磁率的小球在管道内旋转，周期性地切割流量计壳体内永磁铁产生的磁力线，使磁电变换器磁阻周期性变化，导致通过磁感应线圈的磁通量发生变化，在线圈中产生感应电动势，获得交流电压信号输出。该电压频率与小球在管道内的旋转速度相等，磁电转换器输出的交流电压频率与被测体积流量qv的关系式为
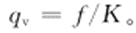（1）
式中：f为交流电压信号的输出频率；K为流量计的仪表系数，一般通过实验标定的方法确定。工程应用中，在测量流量计的输出电压信号的频率后，按照式（1）即可以计算出流体的体积流量。
1.2 噪声分析
受使用环境和设计原理的影响，电磁流量计的输出信号中叠加了一系列的噪声，一个实际的输出信号如图2所示，该信号完全淹没在噪声中。
在一般情况下，实际电磁流量计的输出信号可以表示为
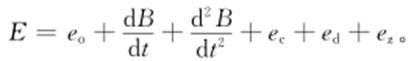（2）
式中：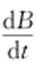
表示微分干扰电压；
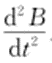表示正交干扰，在相位上与流量计输出信号相差90°。这两种干扰只有在交变磁场中才会产生，电磁流量计采用的是永磁铁，因此这两项干扰为0。eo为输出信号电压；ec为共模干扰电压；ed为极化电压；ez为串模干扰电压。
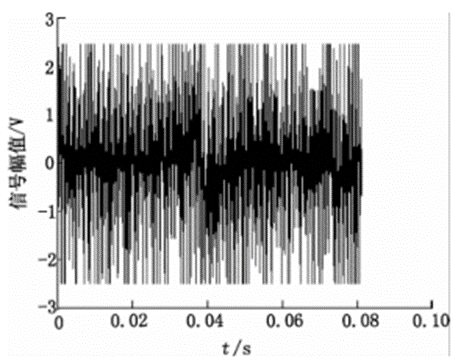
图2 新型流量计输出信号
在电磁流量计中，流量计的原始信号淹没在噪声中，并且信号中含有高频噪声。传统方法采用模拟低通滤波器去除噪声，但是这种方法存在时效性不好和不能动态调节的缺点。而小波阈值去噪算法可以快速给出滤波结果，在保证时效性的同时，最大限度地滤除噪声。
2 小波阈值去噪算法
2.1 小波阈值去噪算法原理
一个含有噪声的信号模型可以表示为
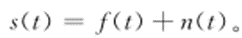（3）
式中：s（t）为含噪信号，即测量信号；f（t）为原始信号，即想恢复的信号；n（t）为噪声。
在噪声服从独立同分布的高斯分布的基础上，提出了一种小波阈值去噪算法，其基本原理是含噪声信号经过小波变换后，真实信号的能量集中在少数小波变换系数上，噪声能量分散在整个小波变换域。从小波变换系数的模来看，真实信号能量集中的小波变换系数的模大于噪声能量所在的小波系数的模。选择合适的阈值，即可以分离真实信号和噪声信号的小波系数，将噪声的小波系数进行适当的处理，然后再进行小波重构，即可以恢复出去噪后的信号。
在含噪信号已经按照Nyquist采样定律抽样成离散序列后，小波阈值去噪算法主要步骤为：①选取小波基；②选择小波阈值和作用阈值函数；③选择变换尺度；④小波重构。小波基函数的选择主要从复值与实值小波、紧支性、对称性、正则性和相似性来考虑。小波阈值和作用阈值函数的选择，目前主流的方法包括：默认阈值规则、基于无偏似然估计的自适应阈值规则以及启发式阈值等。小波尺度选择的原则是在细致刻画信号细节的同时尽量保证信号不失真。
2.2 评价指标
小波去噪效果的评价指标主要有信噪比SNR和均方根误差RMSE，SNR定义如下：
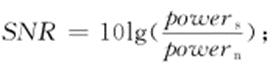（4）
式中：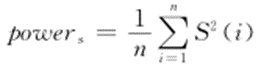
为原始信号的能量；
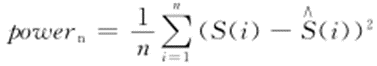为噪声的能量；s（i）为原始信号；
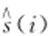表示去噪后的信号的估计值。RMSE定义如下：
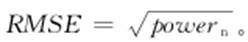（5）
3 实验及分析
软阈值函数和硬阈值函数各有利弊，前者处理相对平滑，但可能造成边缘模糊等影响，后者可以较好地保留图像局部等边缘信息，但是会出现振铃、伪吉布斯效应等失真。本实验采用软阈值函数，利用Matlab的小波处理函数，探讨小波基函数、阈值和变换尺度对小波变换处理新型流量计信号噪声的效果。采集的含噪信号波形如图2所示。
3.1 小波去噪实验
3.1.1 小波基函数对去噪的影响
小波基函数选定为dbN（N＝4，6，8）、symN（N＝4，6，8）和haar，采取强制性去噪，尺度设定为8，去噪效果如图3、4所示。表1为不同小波基下SNR和RMSE的统计数据。
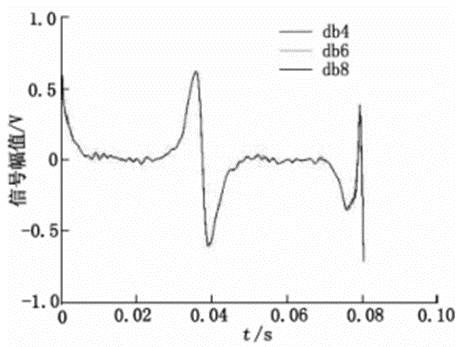
图3 小波基db4，db6和db8重构信号
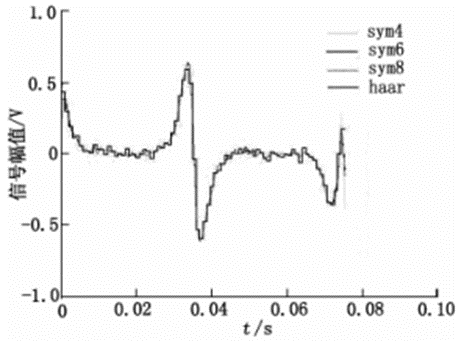
图4 小波基sym4，sym6，sym8和haar重构信号
表1 不同小波基下的SNR和RMSE统计数据
3.1.2 阈值对去噪的影响
小波基函数选定为sym8，尺度设定为8，在不同阈值选择规则下去噪效果如图5～9所示，表2为不同阈值规则下的SNR和RMSE的统计数据。
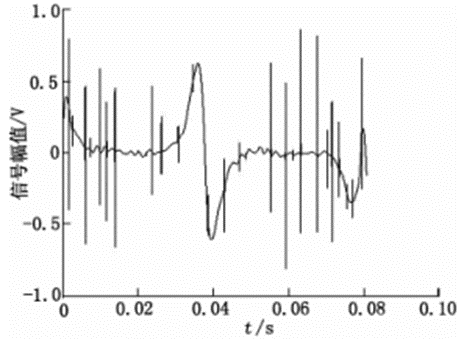
图5 Sqtwolog规则去噪
表2 不同阈值规则下的SNR和RMSE的统计数据
图6 Rigrsure规则去噪
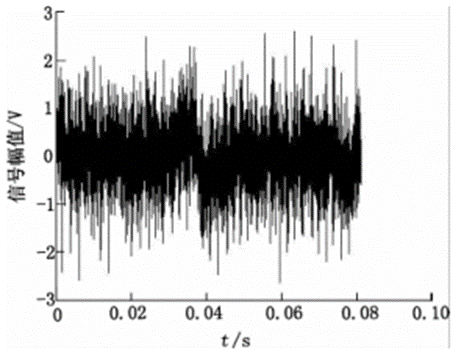
图7 Heursure规则去噪
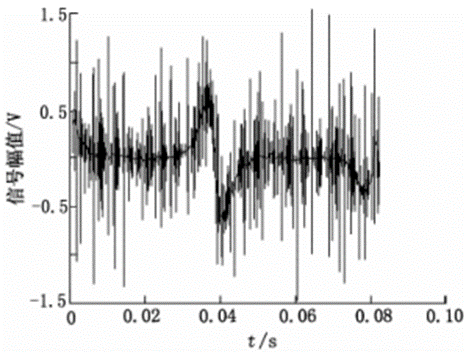
图8 Minimaxi规则去噪
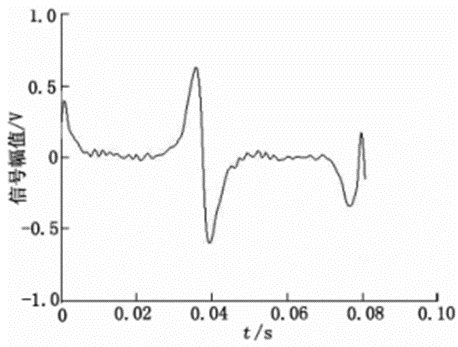
图9 强制规则去噪
3.1.3 变换尺度对去噪的影响
小波基函数选择为sym8，采用强制性消噪。图10～14表示变换尺度从5～9的去噪效果。表3表示不同变换尺度下的SNR和RMSE的统计数据。
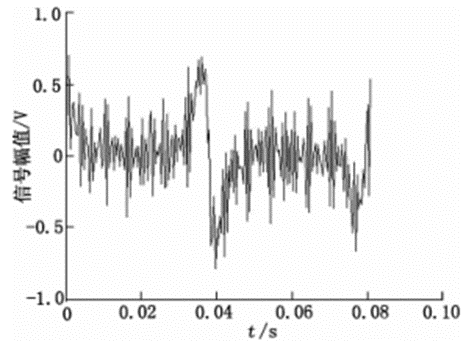
图10 变换尺度5
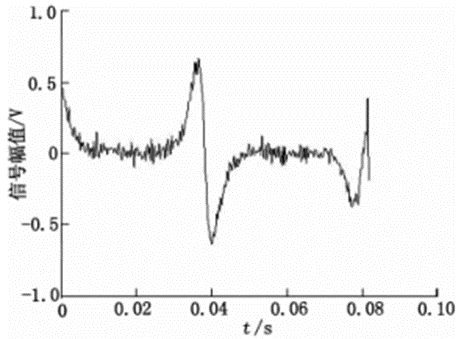
图11 变换尺度6
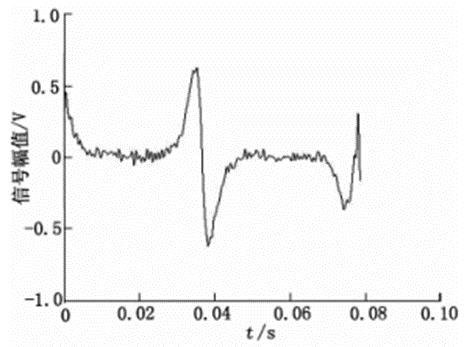
图12 变换尺度7
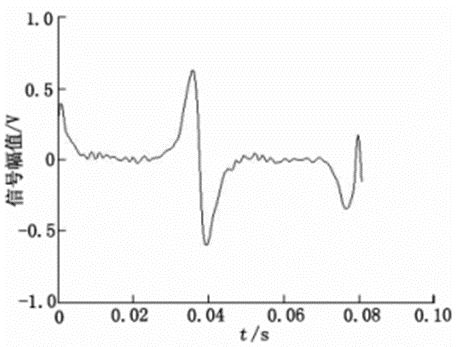
图13 变换尺度8
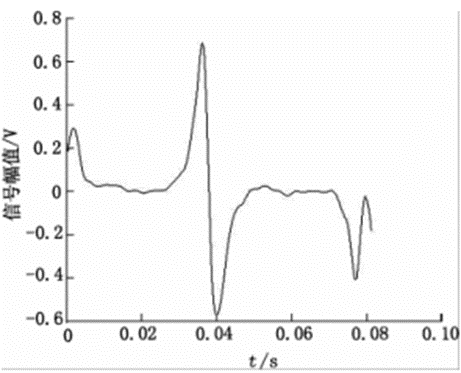
图14 变换尺度9
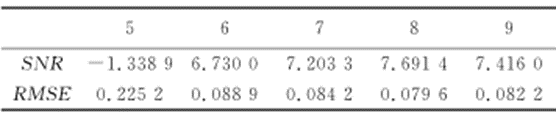
表3 不同变换尺度下的SNR和RMSE的统计数据
3.2 实验结果分析
从表1～3可知，SNR和RMSE均同时达到极值，呈现极强的相关性。从SNR和RMSE的物理意义来看，SNR表示原始信号和噪声的能量比，RMSE表示滤波后信号估计值与原始信号的偏离程度，RMSE越大，说明滤波效果越不明显，滤波后信号中仍有较强的噪声，则滤波后信号的SNR越低。
通过小波基函数对去噪的影响实验可知，在新型电磁流量计输出信号处理中，dbN（N＝4，6，8）和symN（N＝4，6，8）去噪效果较好，输出波形光滑，haar小波在去噪时出现伪－吉布斯现象和锯齿，说明具有消失矩的小波基去噪效果更好；通过比较SNR和RMSE，symN（N＝4，6，8）较dbN（N＝4，6，8）去噪效果更好，sym8去噪效果最优，说明高消失矩的小波基去噪效果更好。
从阈值对去噪的影响实验来看，使用sqt－wolog规则、rigrsure规则、heursure规则和mini－maxi规则去噪后，输出波形中仍然含有大量的毛刺，SNR偏小，RMSE偏大，去噪不完全，说明以上4种方法应用在新型电磁流量计的信号去噪中不合适。强制性去噪的SNR和RMSE最优，去噪效果明显，根据强制性去噪的原理分析，说明新型电磁流量计信号中的主要噪声是高频噪声。
从变换尺度对去噪的影响实验来看，随着变换尺度的增加，SNR增加，RMSE降低，去噪效果越好，但是到一定的程度后，SNR降低，RMSE增加，去噪质量降低。变换尺度为8时去噪效果最好。变换尺度增加，经过阈值去噪的方法处理后，信号细节损失越大，小波重构信号失真变大。综上可知，将小波去噪应用在新型电磁流量计信号去噪时，dbN和symN可以满足要求。在小波基、阈值和变换尺度中，关键的因素是阈值和变换尺度。当小波基采用Sym8、阈值规则采用强制去噪和变换尺度为8时，去噪效果最好。
4 结束语
本文将小波阈值去噪方法引入新型电磁流量计信号处理中，论述了小波去噪的一般步骤，并采用信噪比SNR和均方根误差RMSE作为评价指标，通过实验的方法，分析了小波基、阈值规则和变换尺度对去噪效果的影响。实验结果表明：当小波基采用sym8、阈值规则采用强制去噪和变换尺度为8时去噪效果最好。
